Passkey理论与开发入门
|
245
|
0
|
开发

3277 字
|
15 分钟

通行密钥比密码更易于使用且更安全。采用通行密钥为用户提供一种简单又安全的方式，让用户无需输入密码就能在各种平台上登录你的App 和网站。——Apple

传统密码

远古时代：明文传密码

sequenceDiagram
	autonumber
	participant 用户
	participant 后台
	participant 数据库
	
	Note over 用户,后台: HTTP
	用户 ->> 后台: 1. [注册] 发送用户名A、密码A'
	后台 ->> 数据库: 2. [注册] 保存A、A'
	数据库 ->> 数据库: 3. [注册] 数据库保存A、A'
	
	用户 ->> 后台: 1. [登录] 用户名A，密码X
	后台 ->>+ 数据库: 2. [登录] 提供用户名A
	数据库 ->>- 后台: 3. [登录] 返回正确的用户密码A'
	后台 ->> 后台: 4. [登录] 比较A'和X
	后台 ->> 用户: 5. [登录] 登录成功or失败

优点：

流程直观易懂

风险：

  1. 用户$\Leftrightarrow$后台采用明文通信，易遇到中间人攻击
  2. 数据库一旦被拖库，所有用户的密码会立刻泄漏
  3. 后台能看到用户密码（你以为后台不会打日志吗）

文艺复兴：哈希存密码

sequenceDiagram
	autonumber
	participant 用户（前端）
	participant 后台
	participant 数据库
	
	Note right of 用户（前端）: HTTPS
	用户（前端） ->> 后台: 1. [注册] 发送A、A'
	后台 ->> 数据库: 2. [注册] A、B=hash(A')
	数据库 ->> 数据库: 3. [注册] 数据库保存A、B
	
	用户（前端） ->> 后台: 1. [登录] 用户名A，X
	后台 ->> 数据库: 2. [登录] 提供用户名A
	数据库 ->> 后台: 3. [登录] 返回B
	后台 ->> 后台: 4. [登录] 比较B和X
	后台 ->> 用户（前端）: 5. [登录] 登录成功or失败

优点：

  1. 用户$\Leftrightarrow$后台用HTTPS协议传输，一定程度缓解了中间人攻击的问题
  2. 数据库不明文存用户密码，被拖库后获取用户明文密码存在破解成本，可有效保护用户隐私

风险：

  1. 数据库被拖库后，可用彩虹表推测部分用户密码
  2. 因为哈希值唯一，如果知道用户在其他系统的明文密码，就可以知道用户在该系统中有没有使用相同的密码

彩虹表Wiki

流行：加盐存密码

sequenceDiagram
	autonumber
	participant 用户（前端）
	participant 后台
	participant 数据库
	
	Note right of 用户（前端）: HTTPS
	用户（前端） ->> 后台: 1. [注册] 发送用户名A、密码A'
	后台 ->> 后台: 2. [注册] 为新用户生成盐S
	后台 ->> 数据库: 3. [注册] 将A、S存数据库里
	后台 ->> 数据库: 4. [注册] 计算存储密码B=hash(S+A')
	数据库 ->> 数据库: 3. [注册] 数据库保存A、B
	
	用户（前端） ->> 后台: 1. [登录] 发送用户名A，密码X
	后台 ->> 数据库: 2. [登录] 提供用户名A
	数据库 ->> 后台: 3. [登录] 返回B、S
	后台 ->> 后台: 4. [登录] 比较hash(S+X)==B
	后台 ->> 用户（前端）: 5. [登录] 登录成功or失败

优点：

提高用户密码破解成本

缺点：

盐一旦泄漏，就可用彩虹表推测用户密码

总结：密码永远不安全

2FA：双因素认证

一般而言，三种因素可以证明用户的身份：

  • 秘密信息：例如用户名、密码、口令
  • 个人物品：用户手机、身份证、银行卡
  • 生理特征：指纹、脸、掌纹、虹膜

双因素认证是指需要两个因素证据才能通过认证

TOTP（Time-based one-time password）

基于时间的一次性密码，属于“个人物品”因素

应用

  • QQ令牌
  • 银行密码器
  • 身份认证器APP（微软的Authenticator、谷歌的Authenticator、苹果的Password）

认证原理

算法（前端、后台都会用到）：

TC = floor((unixtime(now) − unixtime(T0)) / TS)
TOTP = HASH(SecretKey, TC)
  • unixtime(now) 当前时间（服务器时间）
  • unixtime(T0) 约定的起始时间
  • TS 验证码有效长度（比如30秒）
  • TC 时间计数器
  • HASH 约定哈希函数，一般是SHA-1
sequenceDiagram
	autonumber
	participant 用户
	participant 后台
	
	Note over 用户,后台: 用户（或设备）与后台协商使用同一个密钥K
	用户 -->> 后台: （用户做了一系列的事情）
	后台 ->> 用户: 请求用户认证
	用户 ->> 用户: 用当前时间、密钥K生成TOTP1
	用户 ->> 后台: 发起认证，发送TOTP1
	后台 ->> 后台: 用当前时间、密钥K生成TOTP2
	后台 ->> 后台: 比较TOTP1、TOTP2
	后台 ->> 用户: 返回认证成功/失败

对于第5、6步，由于客户端时间与服务器时间存在误差，会允许用户使用上n个时间段至下n个时间段的TOTP认证（n由后台决定）

邮箱/短信验证码

太经典了，基本天天都能用到

优点：

  • 可以以安全的名义获取用户隐私

缺点：

  1. 要钱
  2. 链路受控（验证码邮件可能会被收件方屏蔽、短信验证码需通过运营商链路发送）
  3. 接入麻烦，国内接入还需审核短信签名与短信内容
  4. 并非每个人都有可以接收验证码的手机号（比如Github的SMS认证仅限美国用户使用）

Passkey理论

非对称加密

加密和解密使用不同的密钥

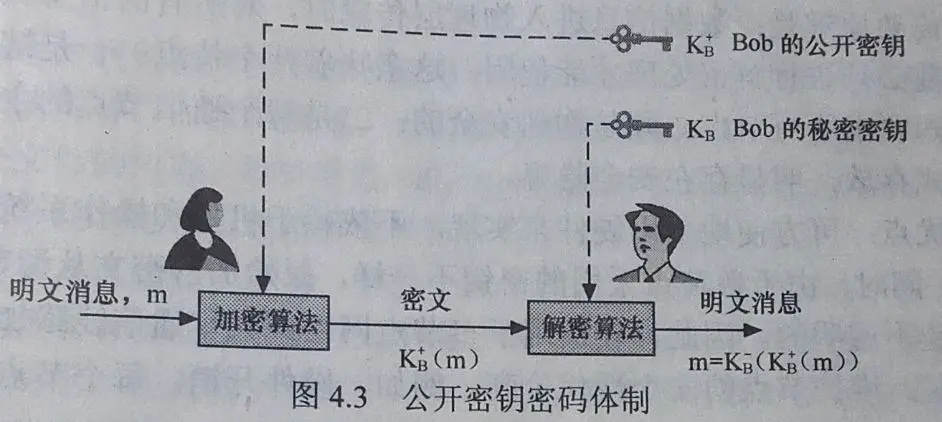
应用：

  • 端对端加密（iMessage）
  • Xlog加密
  • 数字签名

数字签名

数字签名是一种用于验证数字信息完整性、真实性和抗否认性的加密技术，防止信息在传输过程中被篡改。分为签名、验证两步

举例：Alice要告诉Bob，今晚8点开会

不带数字签名：

sequenceDiagram
	autonumber
	actor Alice
	actor Attacker
	actor Bob
	
	Alice ->> Attacker: 发送“今晚8点开会”
	Attacker ->> Attacker: 把信息修改为“今早8点开会”
	Attacker ->> Bob: 发送“今早8点开会”
	Note over Bob: 收到信息: 今早8点开会

Attacker的行为称为“中间人攻击”

带数字签名：

sequenceDiagram
	autonumber
	actor Alice
	actor Attacker
	actor Bob
	
	Alice -->> Alice: 生成公钥、私钥
	Alice -->> Bob: 发送公钥，Bob保存公钥
	Alice ->> Attacker: 发送“今晚8点开会”和签名（用私钥对信息签名）
	Attacker ->> Attacker: 把信息修改为“今早8点开会”
	Attacker ->> Bob: 发送信息“今早8点开会”和签名
	Bob ->> Bob: 验证签名（用公钥验证）
	NOte over Bob: 签名验证失败，说明有人在中间篡改了信息

签名算法（以RSA为例）：

$假设公钥D，私钥E，信息为M，则签名signature=rsa\_encode(E, hash(M))$

$验证签名，rsa\_decode(D, signature) == hash(M)$

RSA详解

Wiki: RSA

前置知识

同余

Wiki: 同余

欧拉定理与欧拉函数

欧拉定理&费马小定理

欧拉函数举例：

$\phi(6)=2$ ，因为1, 2, 3, 4, 5里只有1, 5与6互质

$\phi(7)=1$，因为7是质数，1-6与7互质

$\phi(8)=4$，因为1-8里只有1, 3, 5, 7与8互质

欧拉定理推广
  1. 若a与b互质，则有

$\phi(n) = \phi(a \cdot b) = \phi(a) \cdot \phi(b)$

  1. 若n为质数，则有

$\phi(n) = n – 1$

总结：我们现在有的武器（基础理论）
  1. 欧拉定理：

若 $a$ 和 $n$ 为正整数，且 $a$ 和 $n$ 互质，则
$$
a^{\varphi(n)}\equiv 1\pmod{n}
$$

  1. 欧拉定理推广1:

若 $a$ 和 $b$ 互质，则
$$
\phi(n) = \phi(a \cdot b) = \phi(a) \cdot \phi(b)
$$

  1. 欧拉定理推广2:

若n为质数，则
$$
\phi(n) = n – 1
$$

  1. 费马小定理（实际为欧拉定理推导，可结合 $(1)(3)$ 看 ）

若 $a$ 和 $p$ 为正整数，且 $a$ 与 $p$ 互质，$p$ 为质数，则
$$
a^{p-1}\equiv 1\pmod{p}
$$

密钥生成

第一步 – 输出 $p$ 、 $q$ 、 $n$、$\phi(n)$

取一质数 $p$、$q$，结合 $(2)(3)$，有

$n=pq$

$\phi(n)=\phi(p \cdot q)=\phi(p) \cdot \phi(q) =(p-1)(q-1)$

举例：
p=61, q=53
则n=61*53=3233
\phi(n)=60*52=3120

第二步 – 输出 $e$

选一整数 $e$，满足 $1 < e < \phi(n)$ ，且 $e$ 与 $\phi(n)$ 互质（计算机里一般取65535）

举例：
e=17

第三步 – 输出 $d$

计算出整数 $d$，使得 $ed \equiv 1 \pmod{\phi(n)}$

怎么计算？

$ed \equiv 1 \pmod{\phi(n)}$

$\iff ed = k\cdot\phi(n)+1，k为整数且k>0$

$\iff d = \frac{k\cdot\phi(n)+1}{e}$

举例：
d=2753

第四部 – 汇总

公钥：$(e, n)$

私钥：$(d, n)$

$n$ 的长度：密钥长度（比如RSA1024，1024指的是 $n$ 有1024位）

举例：
上面的公钥：(17, 3233)，私钥：(2753, 3233)

加解密

假设原始数据为 $m$，密文为 $c$，则

公钥加密：$m^{e} \equiv c \pmod{n}$

私钥解密：$c^{d} \equiv m \pmod{n}$

注：$m < n$，否则需分段加密

安全论证

已知公钥，能否知道私钥？

等价于：已知 $n$，$e$，能否知道 $d$？

已知：$ed \equiv 1 \pmod{\phi(n)}$，所以需要知道 $\phi(n)$

已知：$\phi(n)=(p-1)(q-1)$，所以需要知道 $p$，$q$

已知：$n=p \cdot q$，所以需要对 $n$ 做质因数分解

如果 $p$，$q$ 取得比较大（比如1000位），那么 $n$ 至少有 $999+999=1998$位，以人类目前的科学水平不可能对如此大的数做质因数分解。

正确性证明

$已知：m^{e} \equiv c \pmod{n}……..(a)$

$求证：c^{d} \equiv m \pmod{n}……..(b)$

$解：$

$(b)中带入(a)，有m \equiv c^{d} \pmod{n} \equiv m ^ {ed} \pmod{n} \equiv m^{k\phi(n) + 1}\pmod{n}$

$即需证 m \equiv m^{k\phi(n) + 1}\pmod{n}$

$case1: m、n互质$

$根据欧拉定理(1)，有$

$m^{\varphi(n)}\equiv 1\pmod{n} \iff (m^{\varphi(n)})^k \cdot m \equiv 1^k \cdot m \pmod{n} \iff m \equiv m^{k\phi(n) + 1}\pmod{n}$

$秒了$

$case2:m、n不互质$

$已知，n=p \cdot q，而m、n不互质。则必有整数\lambda，使得m= \lambda p或 m = \lambda q。p、q可互换，这里先考虑m=\lambda p$

$由欧拉定理(1)，有$

$m^{\phi(q)} \equiv 1 \pmod{q}$

$\iff (m^{k\phi(q)})^{\phi(p)} \equiv (1^{k\phi(q)})^{\phi(p)} \pmod{q} \equiv 1 \pmod{q}$

$注意到左边(m^{k\phi(q)})^{\phi(p)}=m^{k\phi(n)}，说明有m^{k\phi(n)}\equiv1\pmod{q}，则总有一个正整数r，使得m^{k\phi(n)}=rq+1$

$两边同时乘m=\lambda p，有m^{k\phi(n)+1}=\lambda rpq+\lambda p=\lambda rn+\lambda p$

$等价于m^{k\phi(n)+1}\equiv \lambda p \pmod{n} \equiv m \pmod{n}$

$证毕$

大质数的获取

  1. 随机生成一个大数 $x$
  2. 判断 $x$ 是否为质数，一般选用 $Miller–Rabin素性测试$ 算法判断

素数

Passkey怎么验证用户身份

首先，用户创建一对密钥，私钥存本地，公钥发给服务器并存服务器里。

在登录时，后台会给用户发送挑战（随机字符串）。用户用自己的私钥对挑战做数字签名，并将签名发送给后台。后台再拿存储的用户公钥做验证，判断签名是否有效。

Passkey实践

检测你的设备是否支持Passkey：WebAuthN

流程：简单版

  1. 已注册用户添加Passkey
sequenceDiagram
	autonumber
	participant 前端
	participant 后台
	
	前端 ->> 后台: 请求注册Passkey
	后台 ->> 前端: 返回注册challenge、rpId、支持认证类型、用户特征等
	前端 ->> 前端: 数据透传至浏览器，调用JS创建Passkey
	前端 -->> 前端: 用户完成创建Passkey操作，由密码管理器/物理认证器创建私钥并保存
	前端 ->> 后台: JS返回注册结构体，里面包含公钥、凭据id等
	后台 ->> 后台: 检查挑战是否有效
	后台 ->> 后台: 存储用户公钥

2. 用Passkey登录

sequenceDiagram
	autonumber
	participant 前端
	participant 后台
	
	前端 ->> 后台: 请求用Passkey登录（可携带用户名）
	后台 ->> 前端: 返回登录challenge、rpId、支持的凭据id（如操作1携带用户名请求）
	前端 ->> 前端: 数据透传至浏览器，调用JS获取Passkey认证数据
	前端 -->> 前端: 用户从密码管理器/物理认证器获取私钥，然后生成认证数据
	前端 ->> 后台: JS返回登录结构体，里面包含对challenge的私钥签名、凭据id等
	后台 ->> 后台: 获取Passkey公钥，判断签名、挑战是否有效
	后台 ->> 前端: 登录结果

WebAuthN

WebAuthN是W3C标准。客户端很多Passkey的实现也是基于WebAuthN。MDN Docs

数据结构与流程分析

注册Passkey

客户端请求注册Passkey（用户已登录）：

客户端 -> 后台：随意

后台->客户端:

{
    "challenge": "gVQ2n5FCAcksuEefCEgQRKJB_xfMF4rJMinTXSP72E8",
    "rp": {
        "name": "Passkey Example",
        "id": "example.com"
    },
    "user": {
        "id": "GOVsRuhMQWNoScmh_cK02QyQwTolHSUSlX5ciH242Y4",
        "name": "Michael",
        "displayName": "Michael"
    },
    "pubKeyCredParams": [
        {
            "alg": -7,
            "type": "public-key"
        }
    ],
    "timeout": 60000,
    "attestation": "none",
    "excludeCredentials": [
    ],
    "authenticatorSelection": {
        "authenticatorAttachment": "platform",
        "requireResidentKey": true,
        "residentKey": "required"
    },
    "extensions": {
        "credProps": true
    }
}

W3C: PublicKeyCredentialCreationOptions

  • rp.name，rp.id：域信息
  • user.id：用户特征
  • user.name，user.displayName：Passkey展示在用户密码器上的信息
  • pubKeyCredParams：支持算法类型
  • timeout：challenge有效期时长
  • excludeCredentials：不允许生成的凭据id，通常为用户已注册的凭据id
  • authenticatorSelection：认证类型，可选物理设备/平台

拿到这些数据可以直接透传给系统/浏览器。系统/浏览器会拉起将这些信息透传给密码管理器，让密码管理器创建Passkey。

密码管理器创建Passkey后，会返回公钥及基础信息给系统，系统再透传给客户端/浏览器。

客户端->后台：

{
  "id": "base64url-encoded-credential-id",
  "type": "public-key",
  "response": {
    "clientDataJSON": "base64url-encoded-client-data-json",
    "attestationObject": "base64url-encoded-attestation-object"
  }
}

W3C: AuthenticatorAttestationResponse

  • id：凭据id
  • clientDataJSON：base64编码的json数据，json为：
    • {
       “type”: “webauthn.create”, // 或 “webauthn.get”
       “challenge”: “base64url-encoded-challenge”,
       “origin”: “https://example.com”
      }
  • attestationObject：CBOR格式结构体，包含：
    • authData：凭据信息，CBOR格式的Authenticator data，包含公钥、域信息等W3C: Authenticator data
    • fmt
    • attStmt

后台 -> 客户端：随意

登录

客户端请求登录：

客户端 -> 后台：(可选)用户特征

后台->客户端:

{
    "challenge": "x1wRuShyI4k7BqYJi60kVk-clJWsPnBGgh_7z-W9QYk",
    "allowCredentials": [],
    "timeout": 60000,
    "rpId": "example.com"
}

W3C: PublicKeyCredentialRequestOptions

  • challenge：后台发的挑战
  • allowCredentials：允许使用的凭证id，为空表示由用户自己选择。（如果客户端->后台有发送用户特征，那么这里的allowCredentials应为用户注册过的Passkey凭证id）
  • timeout：挑战过期时间
  • rpId：域信息

客户端拿到这些数据，应直接透传给系统。系统会透传给密码管理器，让密码管理器通过rpId选择一个Passkey。如果没有Passkey，会弹窗告诉用户没有已注册的Passkey。

客户端拿到Passkey认证数据后：

客户端 -> 后台：

{
  "id": "t2hF9lEjZ-8K5oFIZw1wQA",
  "rawId": "dDJoRjlMamp6LTdLNWhGSVp3MXdRQQ",
  "type": "public-key",
  "response": {
    "clientDataJSON": "eyJjaGFsbGVuZ2UiOiJjaGFsbGVuZ2VleGFtcGxlIiwib3JpZ2luIjoiaHR0cHM6Ly93d3cuZXhhbXBsZS5jb20iLCJ0eXBlIjoid2ViYXV0aG4uZ2V0In0",
    "authenticatorData": "YWdhdXRoZW50aWNhdG9yRGF0YS5leGFtcGxl",
    "signature": "c2lnbmF0dXJlZXhhbXBsZQ",
    "userHandle": "dXNlcklkZXh0cmFhcmVv"
  }
}

W3C: AuthenticatorAssertionResponse

  • id：凭据id
  • response.clientDataJSON，response.authenticatorData和注册Passkey时类似
  • signature：用Passkey私钥加密的hash(clientDataJSON|authenticatorData)

后台收到数据后，会先对signature解密，得到B，再判断B==hash(clientDataJSON|authenticatorData)

后台 -> 客户端：随意

iOS实现

Apple Doc: supporting-passkeys

前置条件：

配置associated domains，https://{域名}/.well-known/apple-app-site-association的内容为：

{
    ...
    "webcredentials": {
        "apps": [
            "{团队ID}.{bundleId}"
        ]
    }
}
​

怎么获取团队id？

  1. 打开https://developer.apple.com/account

放上去后：https://m.v.qq.com/.well-known/apple-app-site-association

iPhone启动或安装APP时会去拉一遍数据

需注意的API：

  • ASAuthorizationPlatformPublicKeyCredentialProvider – Passkey注册、认证都要调他
  • ASAuthorizationPlatformPublicKeyCredentialRegistration – Passkey注册结果
  • ASAuthorizationPlatformPublicKeyCredentialAssertion – Passkey认证结果

解析数据：

ASAuthorizationPlatformPublicKeyCredentialRegistration

ASAuthorizationPlatformPublicKeyCredentialAssertion

Android实现

Credential Manager

Android与Passkey的操作都需用到Credential Manager

在Android14以前，安卓的密码管理器只能用谷歌密码管理，而谷歌密码管理是包含在GMS里的。如果系统不带GMS，系统就不会有密码管理器，因此国行系统需要安装谷歌服务才能使用Passkey。

Android14及以后，用户可以安装并使用其它密码管理器了。用户在设置里选择密码器后，如果密码器支持Passkey操作，就可以使用Passkey。

Credential Manager

前置条件：

配置Digital Asset Links，https://{域名}/.well-known/assetlinks.json的内容为：

[
    {
        "relation": [
            "delegate_permission/common.handle_all_urls",
      "delegate_permission/common.get_login_creds"
        ],
        "target": {
            "namespace": "android_app",
            "package_name": "{包名}",
            "sha256_cert_fingerprints": [
                "{指纹签名}"
            ]
        }
    }
]

很简单，无论是登录还是注册，将后台传的数据透传给系统即可

OPPO设备

OPPO自己搞了个SDK：

OPPO PasskeySDK 接入文档

前置条件：

配置fido2-trusted-facets，https://{域名}/.well-known/fido2-trusted-facets.json的内容为：

[
    {
        "relation": [
            "delegate_permission/common.get_login_creds"
        ],
        "target": {
            "namespace": "android_app",
            "package_name": "{包名}",
            "sha256_cert_fingerprints": [
                "{指纹签名}"
            ]
        }
    }
]

OPPO Passkey API和Credential Manager差不多。

咨询OPPO工程师，该API可能很快会被废除：

鸿蒙

不支持，别想了

后台实现

Java库

golang mod

代码略

遇到的坑点：

  • iOS clientDataJSON.origin为https://{associated domains}
  • 安卓 clientDataJSON.origin为 android:apk-key-hash:{包签名base64}
  • OPPO clientDataJSON.origin为 android:apk-key-hash:{包签名base64并做urlEncode}

所以，如果要支持iOS、安卓和OPPO设备的Passkey登录注册，后台需要设置3个origin

本文链接：Passkey理论与开发入门
暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																					

							
							
						

										
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇
下一篇 

                    

                    
			        推荐文章
		            

		            

							
让NAS的WebDAV完美支持HTTPS

							
							

							
Git的一些奇技淫巧

							
							

							
被Xcode15坑麻了

							
							

							
Vision OS 介绍

							
							

							
Go初探 (5) – 结构体与接口

							
							

							
Go初探 (4) – 数组与指针

							
							

							
Go初探 (3) – 基础语句

							
							

							
Go初探 (2) – 文件类型、数据类型、常量与变量

							
							

							
Go初探 (1) – 环境搭建

							
							

							
腾讯云短信的使用